[인공지능]탐색(Search)
인공지능 연구 분야/기술로 Search가 있는데, 왜 Search를 하냐, 또 Search 하는 방법에는 어떤 것들이 있을까에 대해서 작성하려고 한다.
탐색(Search)
: 문제의 해(solution)가 될 수 있는 것들의 집합을 공간(space)으로 간주하고, 문제에 대한 최적의 해를 찾기 위해 공간을 체계적으로 찾아 보는 것이다.
-주요 용어
State(상태) : 특정 시점에 문제의 세계가 처해 있는 모습.
World(세계) : 문제에 포함된 대상들과 이들의 상황을 포괄적으로 지칭.
State space(상태 공간) : 문제 해결 과정에서 초기 상태로 부터 도달할 수 있는, 해가 될 가능성이 있는 모든 상태들의 집합.( Initial state(초기 상태) -> goal state(목표 상태))
State space tree : 상태공간을 변화 같은 것을 그래프로 나타낸 것.
그런데 일반적으로 상태공간을 모두 그리게 되면 굉장히 복잡하고, 메모리문제가 발생하기 때문에 인공지능 탐색에서는 탐색 과정 중에 그래프를 만든다.
=> 종합적으로 왜 탐색(Search)을 굳이 해야하냐면, 여러가지 효율성을 고려해서 탐색을 진행하여야 문제가 발생하지 않기 때문에 문제/상황별로 종류별의 탐색(Search)하는 것이 중요하다.
그러면 어떤 탐색(Search) 방법 들이 있을 까?
4가지로 정리할 수 있다.
1. 맹목적 탐색(Blind Search)
2. 정보 이용 탐색
3. 게임에서의 탐색
4. 제약 조건 만족 문제.
맹목적탐색(무정보 탐색, Blind search)
: 문제의 상태 공간 정보를 이용하지 않고 정해진 순서에 따라 상태 공간 그래프를 점차 생성해 가면서 해를 탐색하는 방법
알고리즘 in Blind Search
1. 깊이 우선 탐색(DFS)
-초기 노드에서 시작하여 깊이 방향으로 탐색
-목표 노드에 도달하면 종료
-더 이상 진행할 수 없으면 , Backtracking(되돌아오는 거)
-방문한 노드는 재방문 하지 않는다
장점 : 메모리 공간 사용이 효율적이다( 루트로 부터 현재 탐색하는 곳까지 기억한다 즉, 공간을 적게 사용한다)
단점 : 어떤 상태에서 노드들을 방문하다보면 무한 루프 가능성이 있고, 그 무한 루프를 돌다 보면 옆에 있는 최적의 노드들을 방문하지 않을 수 있기때문에 최단 경로 탐색을 보장하지 않는다.
2. 너비 우선 탐색(BFS)
-초기 노드에서 시작해서 모든 자식 노드를 확장하여 생성
-목표 노드가 없으면 단말 노드에서 다시 자식 노드 확장.
장점 : 최단 경로 해 탐색을 보장(모든 링크의 길이, 비용이 동일하다고 가정하면)
단점 : 만약 해가 깊이 L에 있을 때, 깊이 L-1까지 모든 경로를 관리하고 있어야 하기 때문에 메모리 공간 사용 비효율적이다.
+깊이 제한 탐색(depth-limited search)

= 깊이 우선 탐색이 무한 루프에 빠질 수 있는 단점을 극복하기 위해 깊이에 한계를 두는 깊이우선 탐색(DFS)
3. 반복적 깊이 심화 탐색(iterative-deepening search)
-DFS는 메모리에 대한 부담은 적지만 최단 경로를 찾는다는 보장이 없고, BFS는 메모리에 대한 부담은 크지만 최단 경로를 찾는 다는 것을 보장한다.
-그 두개의 장점을 합친 것이 반복적 깊이 심화 탐색이다.
-탐색 깊이 한계(Search depth limit)를 0에서 시작하여 점차 1씩 증가시켜 가면서 깊이 우선으로 탐색하여 최단 경로를 찾느 것을 보장한다.

장점 : 메모리 공간 사용 효율적, 최단 경로 해 보장( 모든링크의 길이/비용이 동일한 경우)
-앞에 그림 처럼 반복적으로 노드들이 생성되기 때문에 비효율적인 면이 있으나, 실제로는 비용이 크게 증가하지 않는다.
결론적으로, 맹목적 탐색(Blind search)을 해야 하는 상황에서는 반복적 깊이 심화 탐색 방법을 우선적으로 고려하는 것이 바람직하다.
4. 양방향 탐색(bidirectional search)
-초기 노드와 목표 노드에서 동시에 너비 우선 탐색(BFS)를 진행

-중간에 만나도록 하여 초기노드에서 목표 노드로의 최단 경로를 찾는 방법
장점 : 메모리 공간 사용 효율적(노드당 자식노드가 20개라고 하면, BFS에서 20^20개 노드 생성, Bidirectional Search에서는 2*20^10개의 노드만 생성)
정보이용 탐색(Informed search)
휴리스틱 탐색(heuristic search)
-시간이나 정보가 불충분하여 합리적인 판단을 할 수 없거나 굳이 체계적이고 합리적인 판단을 할 필요가 없는 상황에서 신속하게 어림짐작하여 탐색.
-휴리스틱을 사용하는 탐색 방법으로는 언덕오르기 방법, 최상 우선 탐색, 빔 탐색, A*알고리즘 등이 있다
검색 효율은 좋은데 일반적으로 최적해를 찾는다는 보장은 하지 못한다.
-어떤 휴리스틱을 사용하는 가에 따라 성능 차이가 크게 나타날 수 있다.
1. 언덕 오르기 방법(hill climbing method)
현재 노드에서 확장 가능한 이웃노드들 중에서 휴리스틱에 의한 평가값이 가장 좋은 것 하나만을 선택해서 확장해 가는 탐색 방법.
지역 탐색(local search), 휴리스틱탐색(heuristic search), 그리디 알고리즘(greedy algorithm)이라고도 한다.
DFS나 BFS처럼 여러개의 확장 중인 노드들을 관리하지 않고, 현재 확장 중인 노드만을 관리한다.
출발 위치(상태)에 따라 최적이 아닌 해(낮은 정상 즉 local optimal solution(국소 최적해))에 빠질 가능성이 있다.
(지역탐색이라는 특성을 가졌기 때문에)
2. 최상 우선 탐색(best-first-search)
확장 중인 노드들 중에서 목표 노드까지 남은 거리가 가장 짧은 노드를 확장하여 탐색.
남은 거리를 정확히 알 수 없으므로 휴리스틱(예상치)을 사용하여 추정한다.(greedy하다고 표현)
예)갯수를 계속 최소인 값을 찾아서 움직여본다.(a초기 상태 -> 목표상태)

3. 빔 탐색(beam search)
-휴리스틱에 의한 평가값이 우수한 일정 개수(K)의 확장 가능한 노드만을 메모리에 관리하면서 최상 우선 탐색을 적용
-쉽게 말하면, 전체를 다 돌면 메모리 문제가 발생하니까, 평가 값이 그나마 우수해 보이는 K개 노드만 boundary에 넣는다.
예)K=2이면

4. A*알고리즘??
-앞의 최상우선탐색(best-first-search)를 개선한 것이다라고 할 수 있다. 일반적으로 휴리스틱함수는 어림짐작을 하는 것이지 그렇게 정확한 값을 내는 것이 아니라서 최단의 경로가 아닐 수가 있다는 것이다. 왜냐면은 최상 우선 탐색의 경우에는 전체 거리중의 남은 거리의 최단경로만 가주고 따지기 때문이다. 현재 노드까지 오는 데 걸린 시간은 고려하지 않고 남은 거리의 최단 시간만 추정하고, 오직 남은 최단 경로만 가주고 선택을 한다. 그래서 "남은 경로의 길이 뿐만이 아니라 지금까지 온 경로의 길이도 고려를 하자"해서 나온 것이 A*알고리즘이다.
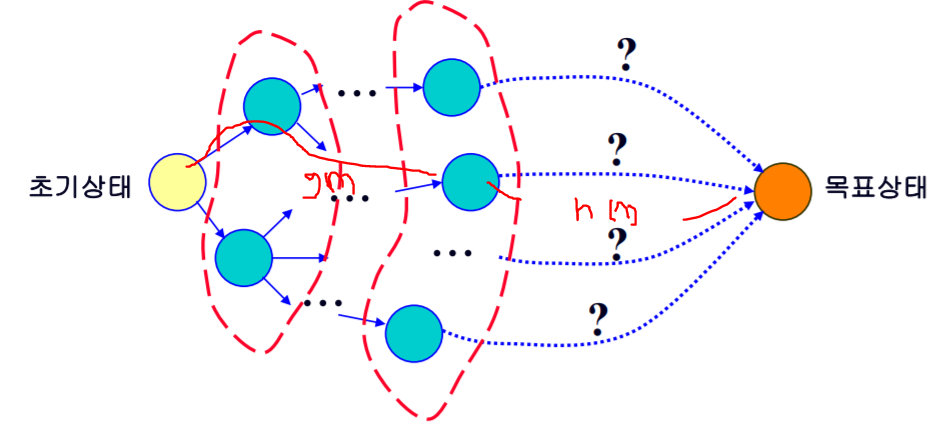
-추청한 전체 비용f^(n)(지금까지 온 경로+앞으로 경로(Best first search))이 최소인 노드를 확장해 가면서 해를 찾는 방법.(f헷트n이라고 부른다)
-노드 n에서 목표 노드까지 남은 비용을 정확히 계산할 수 없기 떄문에 h(n0에 대응하는 휴리스틱 함수h(n)을 사용하여 전체 비용 추정 함수f(n)을 정의한다.
f^(n) = g(n)+h^(n)
(g(n)은 현재까지 탐색한 경로이므로 헤트를 안씌우고, h(n)과 f(n)은 추정 값이므로 헤트를 씌워 표현한다)
f(n)= 노드n을 경유하는 전체 비용, g(n)은 현재노드 n까지 이미 투입된 비용, h(n)은 목표 노드까지 남은 비용
널리 사용되는 대표적인 휴리스티 탐색 알고리즘.
예)
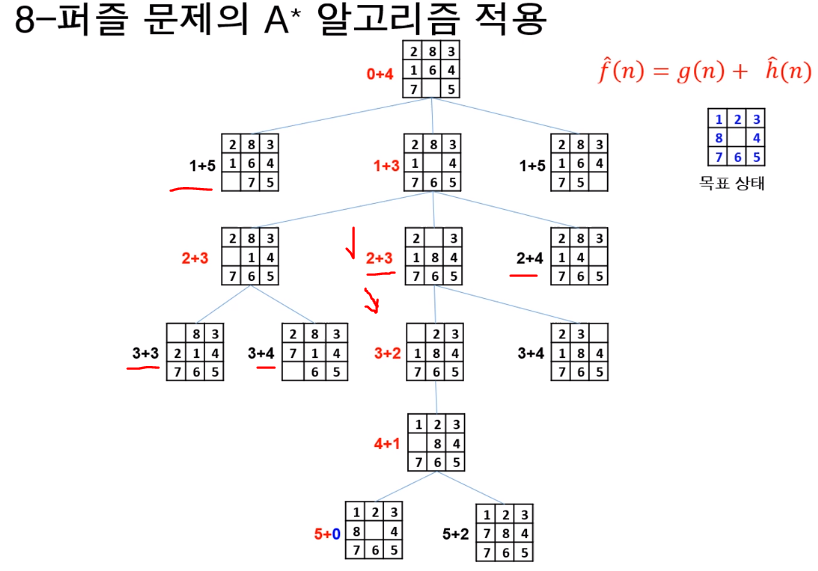
h^(n)이 h(N)보다 크고 불정확하다면, A*알고리즘을 적용하더라도 정확하지 못하다!
최종적으로 h^(n)가 실제 h(n)보다 항상 작거나 같고 A*알고리즘을 적용했을 때, 최적의 해를 만들어 낸다.
게임에서의 탐색
게임트리(game tree)
-상대가 있는 게임에서 자신과 상대방의 가능한 경우의 수(게임 상태)를 나타낸 트리
-틱택토, 바둑, 장기, 체스 등
-게임의 결과는 마지막에 결정
-많은 수(lookahead)를 볼 수록 유리
mini-max 알고리즘

Max 노드는 자신에 해당하는 노드. 자기에게 유리한 최댓값 선택
Min 노드는 상대방에 해당하는 노드, 최솟값을 선택
단말 노드부터 위로 올라가라면서 최소 최대 연산을 반복하여 자신이 선택할 수 있는 방법 중 가장 좋은 값을 결정
일반적으로 게임이 끝나는 시점까지 수를 보기 어렵기 떄문에, 어느 정도 깊이의 수까지 본 다음에 해당 상태에서 유리한 정도를 판정(휴리스틱 이용)하여 이를 바탕으로 최선의 방법을 선택
마지막 층에 있는 모든 노드들까지 다 생성을 해 놓고 단말노드 부터 평가값을 적용해 다시 올라가보는 것인데, 이것을 다 해보지 않더라도 mini-max와 동일한 효과를 얻는 것이 α-β pruning!
α-β 가지치기(α-β pruning)
-깊이 우선 탐색으로 제한 깊이까지 탐색(depth limit search)방식이다.
-max노드, min노드의 개념은 사용한다.
-α : max node type, 커지면 커졌지 작아지지 않는 값
-β : min node type, 작아지면 작아졌지 커지지는 않는 값.
해당깊이에 도달하면 휴리스틱을 사용하여 해당 노드의 상태에 대한 평가값을 계산
현재 노드와 부모노드의 값을 비교하여 검토해 볼 필요가 없는 부분을 탐색하지 않도록 한다
α 자르기(cut-off) = Min노드의 현재값이 부모 노드의 현재 값보다 작거나 같으면, 나머지 자식 노드 탐색 중지.


β 자르기 = Max노드의 현재값이 부모 노드의 현재 값보다 같거나 크면, 나머지 자식 도드 탐색 중지.
정리하면, α-β자르기는 당연한 논리의 경우의 수를 cut-off로 제외시키는 것이다.
몬테카를로 시뮬레이션(ghkrMonte Carlo Simulation)
-몬테카를로 트리 탐색은 몬테카를로 시뮬레이션을 기반을 두고 있는데, 궁극적으로 "탐색 공간을 축소해보면서 탐색을 해보자는 아이디어"이다.
-특정 확률 분포를 기반으로 무작위 표본(random sample)을 생성하고, 이 표본에 따라 행동하는 과정을 반복하여 결과를 확인하고, 이러한 결과확인 과정을 반복하여 최종 결정!

-형세를 판단하여 수치화하는 것이 어려울 때 무작위적인 시뮬레이션에 의해 유리한 정도를 결정하여 게임 트리를 구성하는 (판의 형세판단을 위해)휴리스틱 탐색 방법.
-일정 조건을 만족하는 부분은 트리로 구성, 나머지 가능한 많은 부분을 몬테카를로 시뮬레이션 수행.

mini max 알고리즘과는 다르게 일정 깊이까지 탐색을 하지 않고, 도움이 될 것 같은 부분을 점진적으로 확장해 가며 게임트리를 만들어간다. 어떻게 도움이 될 부분을 판단??
게임 트리의 각 노드에는 해당 노드를 경유해서 게임을 한 횟수(노드 방문 횟수)와 승률 정보가 기록된다.
(선택->확장->시뮬레이션->역전파->선택) 을 반복한다.

*선택(Selection)
-루트 노드로부터 아래로 이동하기 위해 자식 노드를 순차적으로 선택하는 것.
현재까지의 승률이 큰 것과 지금까지 방문횟수가 작은 것을 선호하도록 선택 우선순위를 정한다.
많이 쓰이는 방법은
우선순위를 정할 떄, UCB(Upper Confidence Bound)라는 식을 사용한다. (강화학습할 때도 등장)


*확장(expansion)
단말노드에서 트리 정책에 따라 노드 추가
예: 일정 횟수이상 시도된 수(move)가 있으면 해당 수에 대한 노드 추가
*시뮬레이션 (simulation)
기본 정책(default policy)에 의한 몬테카를로 시뮬레이션 적용
random smovrs또는 약간 똑똑한 방법으로 게임 끝날 때까지 진행
-역전파(backpropagation)
단말 노드에서 루트 노드까지 올라가면서 승점 반영
동작선택 방법

가장 승률이 높은, 루트의 자식 노드 선택
가장 빈번하게 방문한, 루트의 자식 노드선택
승률과 빈도가 가장 큰, 루트의 자식 노드 선택
없으면, 조건을 만족하는 것이 낭로 때까지 탐색 반복
자식 노드의 confidence bound값이 최소값이 가장 큰, 루트의 자식 노드 선택.
정리해보면 , 가능성이 더 높은, 즉 좋아보이는 노드에 대해서 자식노드를 생성하고 트리의 탐색 폭(공간 관리)을 줄이고, 트리 깊이를 늘리지 않기 위해 몬테카를로 시뮬레이션을 적용하는 것이다.
-알파고의 탐색(초장기ver)
알파고의 몬테카클로 트리 검색 : 바둑판 형세 판단을 위한 한가지 방법으로 몬테카를로 트리 검색 사용
무작위로 두는 것이 아니라, 프로 바둑기사들의 기보를 학습한 확장 정책망(rollout policy network)[높은 확률분포]이라는 계산 모델 사용.

->확률에 따라 착수를 하여 몬테카를로 시뮬레이션을 반복하여 해당 바둑판에 대한 형세판단값을 계산,
->별도로 학습된 딥러닝 신경망인 가치망(value network)을 사용하여 형세 판단값을 계산하여 함께 사용
->많은 수의 몬테카를로 시뮬레이션과 딥러닝 모델의 신속한 계산을 위해 다수의 CPU와 GPU를 이용한 분산처리를 진행(AlphaGo zero같은 경우, 몬테카를로 시뮬레이션을 전혀 사용하지 않고 ,강화학습만으로 최고의 성능을 나타내고 있다)
제약조건 만족 문제(constraint satisfaction problem)
: 주어진 제약 조건을 만족하는 조합 해(combinatorial solution)를 찾는 문제
예 n Queen probelm
탐색 기반의 해결 방법
1. backtracking search(백트래킹 탐색)

-깊이 우선 탐색(DFS)를 하는 것처럼 변수에 허용되는 값을 하나씩 대입
-모든 가능한 값을 대입해서 해가 없으면 이전단계로 돌아가서 이전 단계의 변수에 다른 값을 대입
2. constraint propagation(제약조건 전파)
인접 변수 간의 제약 조건에 따라 각 변수에 허용될 수 없는 값들을 제거하는 방식


이렇게 인접 변수의 값을 모두 적은 다음, 안되는 것(제약 조건)을 제거하는 방식이다.
현재 까지 왜 탐색(Search)을 해야 하는지 , 각각 효율성을 위해 어느 알고리즘을 적용하는지에 대해서 특징들을 알아보았습니다.
'AI 기술 정리 > 인공지능(AI) 이론' 카테고리의 다른 글
| 인공지능(AI) 이란? (12) | 2020.09.23 |
|---|

댓글